Векторные диаграммы импульсов в задачах о столкновениях частиц
При заданных ![]() и
и ![]() радиус окружности и положения точек А и В неизменны, а точка С может иметь любое положение на окружности.
радиус окружности и положения точек А и В неизменны, а точка С может иметь любое положение на окружности.
С
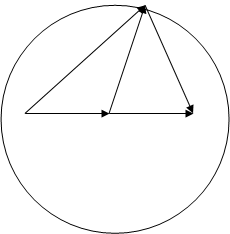
![]()
![]()
![]()
А О В
Рисунок 9.
В частном случае, когда частица с массой ![]() до столкновения покоится в JI-системе, имеем:
до столкновения покоится в JI-системе, имеем:
![]() ,
,![]() , (2.4 13)
, (2.4 13)
т.е. на диаграмме т. В лежит на окружности; ОВ = ОС - радиус, вектор ![]() совпадает с импульсом
совпадает с импульсом ![]() первой частицы до удара. При этом точка А может находиться внутри (если
первой частицы до удара. При этом точка А может находиться внутри (если ![]() ) или вне (если
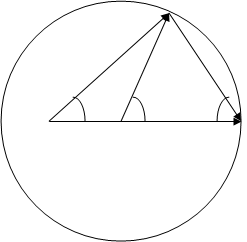
) или вне (если ![]() ) окружности (рисунок 10). Несложно показать, что углы
) окружности (рисунок 10). Несложно показать, что углы ![]() и
и ![]() отклонения частиц после столкновения по отношению к
отклонения частиц после столкновения по отношению к ![]() (к направлению удара) могут быть выражены через угол
(к направлению удара) могут быть выражены через угол ![]() поворота первой частицы в Ц-системе:
поворота первой частицы в Ц-системе:
![]() ,
,![]() , (2.4 14)
, (2.4 14)


 С С
С С
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
А О ![]() В А О
В А О ![]() В
В
Рисунок 10.
Модули скоростей частиц после удара в Л-системе также могут быть выражены через угол ![]() и модуль относительной скорости
и модуль относительной скорости ![]() до удара:
до удара:
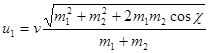 ,
,
![]() . (2.4 15)
. (2.4 15)
Отметим, что сумма ![]() определяет угол разлета частиц после столкновения. При
определяет угол разлета частиц после столкновения. При ![]() эта сумма больше
эта сумма больше ![]() , при
, при ![]() - меньше
- меньше ![]() , угол разлета частиц равной массы прямой.
, угол разлета частиц равной массы прямой.
Педагогические заметки:
Особенности применения уроков оригами в общеобразовательном процессе,
влияющие на психолого-физиологическое развитие младших школьников
Чаще всего оригами преподают детям в детских садах, начальной школе и различных кружках домов творчества. Возможна также работа в частных группах. Задачей таких занятий является не складывание как можно большего количества разнообразных фигурок, а развитие у детей целого ряда способностей и навыков ...
Изучение состояния проблемы правового воспитания в ДОУ
Опытно-исследовательская работа проводилась на базе муниципального дошкольного образовательного учреждения - «Джалильский детский сад №1 «Березка» общеразвивающего вида» Сармановского муниципального района РТ. Предметом исследования были определены формы и методы работы по правовому воспитанию стар ...
Понятия воспитательное пространство и воспитательная система
Социальное пространство воспитательного процесса. Любое явление жизни разворачивается в пространстве, и для каждого свершения существует свое соответствующее пространство. Воспитательный процесс как социально-психологический феномен конструируется, располагается и развивается во вполне определен ...
Категории
- Главная
- Трудовое воспитание в семье
- Современные реалии детства
- Основы правового воспитания дошкольников
- Развитие воображения
- Педагогика как наука
- Развитие речевого дыхания
- Информация о педагогике

