Векторные диаграммы импульсов в задачах о столкновениях частиц

Остановимся на механическом описании процессов неупругого и упругого соударений, имеющем прикладное значение в разных разделах физики. Рассмотрим сначала "самопроизвольный" (без воздействия внешних сил) распад частицы на две составные части - на две частицы, движущиеся после распада независимо друг от друга. Наиболее просто процесс выглядит в системе отсчета, в которой частица до распада покоилась; в этой системе будет покоиться центр масс двух образовавшихся после распада частиц. Назовем эту систему отсчета Ц-системой. По закону сохранения импульса сумма импульсов обеих образовавшихся после распада частиц в Ц-системе равна нулю, т.е. импульсы частиц равны по модулю и направлены в противоположные стороны Модуль импульса каждой частицы определяется из закона сохранения энергии:

(2.4 1)

где и - массы образовавшихся частиц, и - их внутренние энергии, - внутренняя энергия исходной частицы. Тогда энергия распада

. (2.4 2)

Распад возможен при ε>0. Из (2.4 1) и (2.4 2) находим:

(2.4 3)

где - приведенная масса образовавшихся частиц. Скорости частиц после распада в Ц-системе: и .

Перейдем к системе отсчета, в которой первичная частица движется до распада со скоростью . Эту систему отсчета обычно называют лабораторной системой (JI-системой). Пусть скорость одной из частиц после распада в JI-системе равна , а в Ц-системе равна . Тогда

или ; (2.4 4), , (2.4 5)

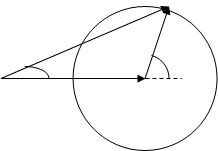
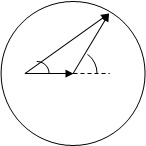
где - угол выпета частицы по отношению к направлению скорости . Зависимость скорости распадной частицы от направления ее вылета в JI-системе может быть представлена с помощью диаграмм (рисунок 8).

A А

О О

Рисунок 8.

Из рисунка 8 видно, что при частица может вылететь под любым углом ; при - только вперед под углом, где

Педагогические заметки:

Специфические особенности жанрового многообразия детского фольклора
Так как в фольклоре имеет место сотворчество множества певцов и рассказчиков, то на первый план выдвигается не только отдельные изменяющиеся произведения – результат работы многих людей, но и то общее, что объединяет отдельные произведения в группы – жанры. Особенности жанра сохраняются каждым твор ...

Проблема интеграции детей с ограниченными возможностями здоровья в образовательную систему РФ
Интегрированное (совместно с нормально развивающимися сверстниками) обучение предполагает овладение ребенком с отклонениями в развитии общеобразовательным стандартом в те же (или близкие) сроки, что и здоровыми детьми. Исследования показывают, что интегрированное обучение может быть эффективным для ...

Цель, задачи, методика констатирующего эксперимента и его результаты
Целью констатирующего этапа эксперимента являлось выявление особенностей развития мыслительных операций у детей 6–7 лет с нарушениями зрения. В процессе проведения констатирующего эксперимента перед нами стояли следующие задачи: 1) определение уровня развития мыслительных операций у детей 6–7 лет с ...