Векторные диаграммы импульсов в задачах о столкновениях частиц

. (2.4 6)

Легко установить связь между углами вылета в JI-системе и в Ц-системе:

, (2.4 7)

причем если при каждому значению соответствует одно значение , то при каждому значению соответствует два значения (за исключением случая ).

Перейдем к изучению столкновений частиц. Задача о неупругом столкновении двух частиц обратна задаче о распаде частицы на две, рассмотренной выше. В Ц-системе справедливо выражение (2.4 1), а величина в этом случае равна приращению внутренней энергии составной частицы, образовавшейся в результате неупругого столкновения.

Рассмотрим задачу об упругом столкновении двух частиц, при котором не изменяется их внутреннее состояние. Как известно, в JI-системе скорость центра масс двух частиц с массами и скоростями и определяется выражением:

. (2.4 8)

Скорости частиц до столкновения в Ц-системе связаны с их скоростями в JI-системе известными соотношениями

, , (2.4 9)

где . В силу закона сохранения импульса импульсы обеих частиц в Ц-системе остаются после столкновения равными по модулю и направленными в противоположные стороны, в силу закона сохранения энергии модули импульсов в Ц - системе при столкновении не меняются. Таким образом, в Ц-системе результат столкновения сводится лишь к повороту скоростей обеих частиц, причем после поворота скорости остаются направленными в противоположные стороны. Если единичный вектор выражает направление скорости первой частицы после столкновения, то в Ц-системе.

,. (2.4 10)

Чтобы вернуться к JI-системе, нужно к этим выражениям добавить скорость центра масс:

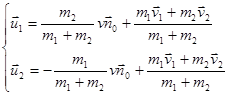(2.4 11)

Этим исчерпываются сведения, которые можно получить из одних только законов сохранения импульса и энергии. Направление вектора зависит от условий взаимодействия частиц (от взаимного расположения во время столкновения и т.п.).

Для геометрической интерпретации результатов перейдем опять к импульсам. Из (2.4 11) получим:

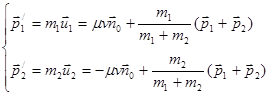(2.4 12)

где - приведенная масса частицы. Векторная диаграмма импульсов, соответствующая (2.4 12), приведена на рисунке 9. Здесь

,,.

Педагогические заметки:

Методика проведения занятий по формированию технических навыков и умений у детей старшего дошкольного возраста на формирующем этапе эксперимента
Программа по изобразительной деятельности в детском саду предусматривает решение следующих задач: воспитывать интерес к художественной деятельности, развивать восприятие, воображение, формировать образные представления, развивать творческие способности, учить способам создания изображений. На занят ...

Примерный алгоритм обучения просмотровому чтению
Внимательно прочитайте заголовок текста, постарайтесь вникнуть в его смысл, определить главную мысль текста. Прочитайте первое предложение текста. Сопоставьте его содержание с заголовком. Прочитайте первый абзац. Сопоставьте его содержание со своим представлением о главной мысли текста. Просмотрите ...

Понятие ритмопластики в современной психологической литературе
По определению Зинкевич-Евстигнеевой Т. «ритмопластика» подразумевает нахождение внутреннего ритма, сообразного природе человека. У каждого человека есть свой ритм: ритм дыхания, сердцебиения, циркуляции крови, бодрствования и сна. Внутренний ритм предопределяет темп жизни, стремления, мотивацию, в ...