Анализ учебников по теме «Четырехугольники» в школьном курсе математики основной школы

Ромб также является параллелограммом, следовательно, он обладает всеми его свойствами. Приводится доказательство признака ромба (если в параллелограмме диагонали перпендикулярны, то это ромб).

Квадрат определяется через прямоугольник. Авторы отмечают, что квадрат также является ромбом, у которого все углы прямые. На основании этого следует, что квадрат обладает всеми свойствами прямоугольника и ромба.

Перед изучением трапеции авторы рассматривают теорему о средней линии треугольника. Дают определение средней линии треугольника и приводят доказательство теоремы. Этот шаг оправдан, так как при доказательстве теоремы о средней линии трапеции используется теорема о средней линии треугольника. Определение трапеции такое же, как и в других учебниках. Трапецией называется четырехугольник, у которого две стороны параллельны. Дается определение равнобокой, прямоугольной трапеций, средней линии трапеции. Приводится доказательство теоремы о средней линии трапеции и рассматривается следствие из данной теоремы.

В конце главы приводится доказательство теоремы Фалеса, которая является обобщением теорем о средней линии треугольника и трапеции. В конце каждого параграфа и главы приводятся вопросы и задачи для проверки ЗУН учащихся.

3 «Геометрия, 7–11 класс», автор А.В. Погорелов

Тема «Четырехугольники» изучается в восьмом классе. Этой теме в учебнике посвящен шестой параграф.

В первом пункте параграфа дается определение четырехугольника и предлагается задача на усвоение определения. Рассказывается, какие стороны и вершины называются соседними и противоположными. Дают определение диагоналей и периметра четырехугольника

В следующих пунктах дается определение параллелограмма, прямоугольника, ромба и квадрата. Определение прямоугольника и ромба даются на основе параллелограмма. Доказывается признак параллелограмма. Доказываются свойства параллелограмма, прямоугольника и ромба. Рассматривается по одной задаче на каждое свойство параллелограмма. Для ромба и прямоугольника предлагаются задачи на использование определения. Определение квадрата дается на основе прямоугольника. Так же говорится, что квадрат является ромбом, так как стороны квадрата равны. На основе этого делается вывод, что квадрат обладает свойствами прямоугольника и ромба. Приводится пример использования определения при решении задачи.

Так же в данном параграфе изучается теорема Фалеса и средняя линия треугольника. После приведения доказательства теоремы Фалеса автор делает замечание, что в качестве сторон угла можно взять любые две прямые. Предлагается задача разделить отрезок на n равных частей. При изучении средней линии треугольника дается определение и доказательство теоремы о средней линии треугольника.

В следующем пункте рассматривается еще один вид четырехугольника – трапеция. Вводятся определения трапеции и средней линии трапеции. Доказывается теорема о средней линии трапеции.

В последних пунктах параграфа доказывается теорема о пропорциональных отрезках и рассказывается, как построить четвертый пропорциональный отрезок.

4 «Геометрия, 7–9 класс», автор И.Ф. Шарыгин

Тема «Четырехугольники» изучается в главе «Подобие».

Первый параграф данной главы посвящен теме «Параллелограмм, прямоугольник, ромб, квадрат».

Свойства и признаки параллелограмма объединены в одну теорему, доказательство которой здесь же приводится. Автор отмечает, что из определения прямоугольника следует параллельность его противоположных сторон, то есть прямоугольник является частным случаем параллелограмма. Приводится доказательство теоремы о свойствах прямоугольника.

Свойства и признаки ромба также объединены в одну теорему, доказательство которой здесь же приводится. Автор отмечает, что квадрат обладает всеми свойствами прямоугольника и ромба, так как он является и прямоугольником, и ромбом. Еще один вид четырехугольника, а именно трапеция, изучается после теоремы Фалеса и теоремы о средней линии треугольника. Трапеция определяется как четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Определены термины основания, боковые стороны трапеции. Доказана теорема о средней линии трапеции.

Таким образом, изучение четырехугольников идет по следующей схеме:

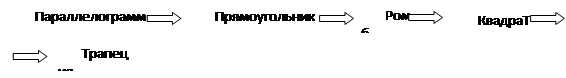
Проведенный анализ позволяет сделать следующие выводы:

в каждом учебнике свой порядок изучения частных видов четырехугольников

в каждом учебнике представлен большой объем упражнений для закрепления основных знаний, умений и навыков по данной теме.

Педагогические заметки:

Элементы педагогической технологии
Педагогическая технология как система научного знания должна оптимизировать и обеспечить воспитательный процесс. Воспитание – это объективный процесс, который совершается в обществе независимо от воли и желания педагога. Развитие личности не прекращается ни на минуту. Задача педагога заключается в ...

Реализация конвенции о защите прав ребенка в ДОУ
Происходящие в Российской Федерации процессы общественно-политических и социально-экономических преобразований выдвинули ряд важных, качественно новых задач по созданию суверенного, экономически развитого, цивилизованного, в полном смысле слова демократического государства, обеспечивающего на деле ...

Использование современных педагогических технологий по формированию и развитию творческого студенческого коллектива
Творческая деятельность – важнейший вид духовной деятельности человека, эффективность которой обуславливается сочетанием мотивационно-целевой, операционной, содержательной, когнитивно-творческой составляющих, направленных на проявление и реализацию индивидуальности. Среди видов искусства, оказывающ ...