Анализ учебников по теме «Четырехугольники» в школьном курсе математики основной школы

Понятие четырехугольник вводится в зависимости от того, как и когда введено понятие многоугольника:

в учебнике Л.С. Атанасяна четырехугольник вводится как частный вид многоугольника;

в учебнике А.В. Погорелова понятие многоугольника вводится значительно позже, поэтому дается определение, аналогичное определению треугольника: «Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не должны пересекаться». Сайт, ссылка на кракен тор.

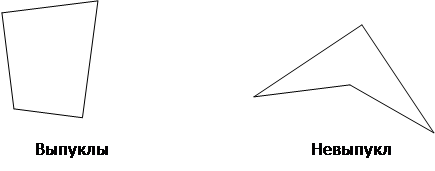
В теме «Четырехугольники» рассматриваются выпуклые и невыпуклые четырехугольники. Для более наглядного представления полезно составить следующую схему:

Основанием для классификации выпуклых четырехугольников является наличие параллельных сторон: в случае одной пары параллельных сторон из класса четырехугольников выделяется множество трапеций, в случае двух пар параллельных сторон – множество параллелограммов.

Структурно – логическая схема основных классов геометрических фигур, составляющих её, имеет вид:

При классификации всех четырехугольников за основание классификации принимается сначала взаимное расположение противоположных сторон – не параллельность или параллельность их, вследствие чего множество всех выпуклых четырехугольников разбивается на три класса:

четырехугольники, не имеющие параллельных сторон;

трапеции (одна пара параллельных сторон);

параллелограммы (две пары параллельных сторон).

За основание классификации параллелограммов принимается равенство или неравенство смежных сторон (собственно параллелограммы и ромбы), а также отсутствие или наличие прямого угла (собственно параллелограммы и прямоугольники).

В основу классификации ромбов кладется отсутствие или наличие прямого угла (собственно ромбы и квадраты).

При классификации прямоугольников за основание принимается равенство или неравенство смежных сторон (собственно прямоугольники и квадраты).

Классификация трапеции проводится сначала по длине боковых сторон (равнобокая и неравнобокая трапеции); затем неравнобокие трапеции в свою очередь разбиваются на прямоугольные и непрямоугольные.

Описанный процесс составления классификации четырехугольников, в частности выпуклых четырехугольников, в основу которого положена последовательная целенаправленная деформация каждой вновь полученной фигуры (получить сначала параллельные, а потом и равные стороны, затем прямые углы), позволяет отчетливо выяснить генетический характер образования каждого частного вида выпуклых четырехугольников. Из четырехугольника с непараллельными сторонами получаются трапеции и параллелограммы, из параллелограммов – прямоугольники и ромбы, из ромбов и прямоугольников – квадраты.

Выяснение этого генезиса – происхождения одной фигуры из другой – помогает более отчетливому восприятию самих геометрических образов, выяснению связей между ними, а в силу этого позволяет распространять свойство одной более общей фигуры, например параллелограмма, на частные виды ее, на прямоугольник, ромб и квадрат. Представим это на схеме. Такую схему полезно использовать при обучении школьников.

Во всех действующих в настоящее время пособиях осуществляется одинаковый подход во введении частных параллелограммов: прямоугольников, ромбов и квадратов. Частные виды четырехугольников рассматриваются в соответствии с условной единой методической схемой:

дается определение (через ранее изученный вид четырехугольников);

указываются элементы;

формулируются и доказываются свойства и признаки;

рассматривается задача на построение этого четырехугольника.

Квадрат в одних учебниках вводится как четырехугольник, который одновременно является прямоугольником и ромбом. В других – квадрат определяется как частный вид прямоугольника. В большинстве учебников трапеция рассматривается после параллелограмма и его частных видов. Тема имеет большие возможности для развития логического мышления.

легко выявляется логическая структура темы. Полезно использовать структурно-логические схемы;

используются формально-логические определения (через ближайший род и видовое отличие).

Определить понятие, значит перечислить его существенные свойства, а это зачастую бывает нелегко. Однако, задача упрощается, если использовать ранее изученные понятия. Сказанное обусловило способ определения понятия, называемый «через ближайший род и видовое отличие». Конструирование определения этим способом заключается в следующем:

Указывается род, в который входит определяемое понятие как вид.

Педагогические заметки:

Методические рекомендации по использованию метода проектов как средство развития речевых умений
Проекты, предназначенные для обучения языку, обладают как общими для всех проектов чертами, так и отличительными особенностями, среди которых главными являются следующие: 1. использование языка в ситуациях, максимально приближенных к условиям реального общения; 2. акцент на самостоятельной работе у ...

Детское творчество, его основная задача
Детское творчество присутствует в нашей действительности повсюду: на асфальте улиц, на заборах, на стенах домов; работы детей хранят в школах, семьях и музеях, их печатают в книжках и журналах. Многие люди, давно простившиеся со своим детством, сберегают их в своих личных архивах. Кто бывал на выст ...

Анализ и интерпретация результатов опытно-экспериментальной работы
Интересны итоги БОУ-обсуждений курсантами значимости различных социально-педагогических условий эффективности воспитания патриотизма приводимые в таблице 3. Как видно из данных этих опросов воспитуемые считают наиболее важными социально-педагогическими условиями восприятия патриотического мировоззр ...