Анализ учебников по теме «Четырехугольники» в школьном курсе математики основной школы

В 5 и 6 классах школьники также встречаются с четырехугольниками. Как и в начальной школе, изучение идет поверхностно. К прямоугольнику и квадрату добавляются параллелограмм и трапеция.

Более подробно тема «Четырехугольники» изучается в курсе геометрии в восьмом классе. Рассмотрим, как предлагается изучение данной темы разными авторскими коллективами в учебниках геометрии, рекомендованных Министерством образования РФ.

1 «Геометрия, 7–9 класс», автор Л.С. Атанасян

Тема «четырехугольники» изучается в начале восьмого класса. На её изучение отводится целая глава. Первый параграф данной главы посвящен многоугольникам. Дается определение многоугольника (п. 39), а также что называют вершинами и сторонами многоугольника. Говорится, что называется n-угольником. Приводятся примеры фигур, которые являются многоугольниками и тех, которые не являются многоугольниками. Дается определение соседних вершин и диагоналей многоугольника. В конце данного пункта говорит о том, что любой многоугольник разделяет плоскость на две части (внутренняя и внешняя область многоугольника).

В следующем пункте первого параграфа (п. 40) автор рассказывает о выпуклых многоугольниках. Приводит пример выпуклого и невыпуклого многоугольника. Рассматривая выпуклый n-угольником A1A2A3…An-1AnA1 автор говорит, что углы AnA1A2, A1A2A3, …, An-1AnA1 называются углами этого многоугольника и показывает чему равняется сумма углов выпуклого n-угольника.

Последний пункт данного параграфа посвящен четырехугольнику. Автор не дает определения четырехугольника, он просто говорит, что четырехугольник имеет четыре вершины, четыре стороны и две диагонали. Дает определение противоположных сторон и вершин. Приводит пример выпуклого и невыпуклого четырехугольника. На основании суммы углов выпуклого n-угольника делается вывод, что сумма углов выпуклого четырехугольника равна 360є.

Второй параграф посвящен параллелограмму и трапеции. При изучении параллелограмма дается его определение, и доказываются его свойства. Л.С. Атанасян предлагает другой способ доказательства свойств параллелограмма по сравнению с учебником. Данные доказательства являются меньшими по объему и легче усваиваются учениками.

В следующем пункте параграфа рассказывается о признаках параллелограмма. В отличие от А.В. Погорелова Л.С. Атанасян рассматривает три признака параллелограмма. Это позволяет быстрее решать задачи на доказательство.

Последний пункт параграфа отводится трапеции. В этом пункте дается определение трапеции и рассматриваются виды трапеции. В этом учебнике также предлагается для изучения теорема Фалеса, но в явном виде она не выделена отдельным пунктом.

Третий параграф посвящен прямоугольнику, ромбу и квадрату. Определение прямоугольника и ромба даются на основе параллелограмма. Так как прямоугольник и ромб являются параллелограммом, то они обладают всеми свойствами параллелограмма. Также в учебнике рассматривается особые свойства прямоугольника и ромба. Определение и свойство квадрата рассматриваются подобно, что и в учебнике, добавляются особые свойства квадрата.

В конце параграфа отдельным пунктом выделена осевая и центральная симметрия. В конце главы предлагаются задачи на отработку ЗУН.

Изучение четырехугольников в учебнике Л.С. Атанасяна идет по следующей схеме:

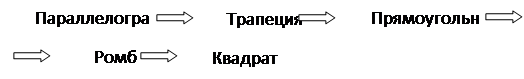
2 «Геометрия, 7–9 класс», авторы И.М. Смирнова, В.А. Смирнов

Тема «Четырехугольники» изучается в восьмом классе в главе «Параллельность».

В первом параграфе рассматриваются параллельные прямые. Дается определение параллельных прямых, секущей. Определяются соответственные, внутренние накрест лежащие и внутренние односторонние углы. Доказывается признак параллельности двух прямых, и рассматриваются три следствия данной теоремы. Также доказывается теорема о равенстве внутренних накрест лежащих углов.

Следующий параграф посвящен сумме углов многоугольника. Сначала доказывается, что сумма углов треугольника равна 1800, а затем переходят к доказательству общего случая.

В третьем параграфе рассматривают параллелограмм. Дается определение параллелограмма, доказывается три его свойства. Рассмотрен пример на применение свойств параллелограмма. На признаки параллелограмма отводится четвертый параграф, в котором доказываются первый и второй признаки параллелограмма. Приведено два примера на применение данных признаков.

В пятом параграфе рассмотрены прямоугольник, ромб и квадрат. Прямоугольник и ромб определяются через параллелограмм. Авторы отмечают, что прямоугольник является частным случаем параллелограмма. Поэтому он обладает всеми свойствами параллелограмма и приводят доказательство признака прямоугольника (если в параллелограмме диагонали равны, то это прямоугольник).

Педагогические заметки:

Какие стороны работы университета требуют совершенствования
Накануне Нового года президент Дмитрий Медведев подписал указ «О мерах по совершенствованию деятельности органов внутренних дел Российской Федерации». Документ предусматривает сокращение численности сотрудников органов внутренних дел до 1 января 2012 года на 20%. В связи с этим некоторые СМИ сообщи ...

Сущность деятельности педагога дополнительного образования в области профессиональной ориентации школьников
В настоящее время система профориентационной работы педагога дополнительного образования включает в себя деятельность по следующим направлениям: 1. Профессиональное просвещение, включающее профинформацию, профпропаганду и профагитацию. 2. Предварительная профессиональная диагностика, направленная н ...

Психологические особенности развития речи детей дошкольного возраста
Все исследователи, изучающие проблему развития связной речи, обращаются к характеристике, которую дал ей С.Л.Рубинштейн. Именно ему принадлежит определение ситуативной и контекстной речи. Рубинштейн отмечал, что для говорящего всякая речь, передающая его мысль или желание, является связной речью (в ...