Конспекты факультативных занятий «Четырёхугольники их свойства и признаки»

Применение знаний о свойствах четырехугольников при решении практических задач

Цели: 1. Развитие мыслительной деятельности при решении практических задач по теме «Четырехугольники».

2. Развитие творческих способностей, логического мышления.

3. Формирование и закрепление комбинаторных навыков учащихся.

План

1. Кросснамбер «Многоугольники».

2. Составьте четырехугольники.

3. Проверка домашнего задания.

4. Практическая работа.

5. Решение практических задач.

6. Сказка-вопрос.

7. Пентамино.

8. Подведение итога занятия.

Кросснамберы – один из видов числовых ребусов. В переводе с английского слово «кросснамбер» означает «кресточислица».

При составлении кросснамберов применяется тот же принцип, что и при составлении кроссвордов: в каждую клетку вписывается один знак, «работающий» на горизонталь и на вертикаль.

В каждую клетку «кресточислицы» вписывается по одной цифре. Чтобы не было путаницы, номера заданий обозначают буквами. Числа, подлежащие отгадыванию, – только целые положительные; запись таких чисел не может начинаться с нуля.

Некоторые задания из кросснамберов могут показаться расплывчатыми и допускающими несколько (а иногда и очень много) ответов. Например: «Составное число, каждая цифра которого – простое число». Но таков стиль кросснамберов и кроссвордов. Если бы они всегда давали только однозначные ответы, то это не было бы игрой. Если ученик не может понять, что от него требует данное описание, пусть он посмотрит на числа, пересекающиеся с данным. Где-то обязательно найдется подсказка.

Задание. Составьте четырехугольники

Каждому ученику дан набор равнобедренных прямоугольных треугольников, которые между собой равны. Кто быстрее составит всевозможные четырехугольники?

Проверка домашнего задания

Квадрат разрезали на 7 частей. Сложите из этих частей: а) прямоугольник; б) параллелограмм; в) трапецию (рис. 1).

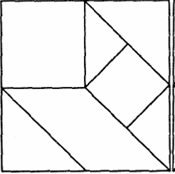
Рисунок 1

Практическая работа

Каждому ученику раздается несколько листов произвольной формы (круг, квадрат, прямоугольник).

Задание. Путем нескольких перегибов получить известные нам четырехугольники, используя их определения, свойства.

Решение практических задач

1. Деревни А, В, С, D расположены в вершинах прямоугольника. В каком месте следует построить мост через реку, чтобы он был одинаково удален от всех деревень?

2. Как провести через пункт N дорогу, чтобы расстояния по ней от этого пункта до железной дороги и до канала были равными? (рис. 2)?

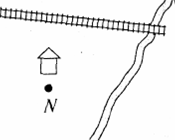
Рисунок 2

3. Жители трех домов, расположенных в вершинах равнобедренного треугольника с углом 120°, решили построить общий колодец. Какое место для колодца им следует выбрать, чтобы все три дома находились от него на одинаковом расстоянии?

4. В центре площади расположен фонтан, около которого надо разбить 4 одинаковых клумбы с розами. Как рассадить 36 кустов роз – по 10 кустов на каждой клумбе – с таким расчетом, чтобы фонтан был одинаково удален от всех клумб?

Ответы и решения (с указаниями способов решения).

1. Используйте свойство диагоналей прямоугольника.

2. Используйте свойство диагоналей прямоугольника.

3. Достройте до ромба с вершинами АВСD. Тогда колодец надо строить в точке D.

4. Фонтан находится в центре квадрата. 36 кустов роз по 10 в каждой клумбе рассаживаются на сторонах этого квадрата.

Сказка-вопрос

Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и никак не могли прийти к единому мнению. Тогда один старый параллелограмм сказал: «Давайте отправимся все в царство четырехугольников. Кто туда первым придет, тот и будет королем». Все согласились. Рано утром отправились они в далекое путешествие. На пути путешественников повстречалась река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам». Часть четырехугольников остались на берегу, остальные благополучно переплыли и отправились дальше. На пути им встретилась высокая гора, которая сказала, что даст пройти дальше только тем, у кого диагонали равны. Несколько путешественников осталось у горы, остальные продолжили путь. Дошли они до большого обрыва, через который был переброшен узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и был провозглашен королем.

Педагогические заметки:

Система работы по формированию познавательного интереса учащихся на уроках русского языка с помощью наглядных пособий
Умение использовать наглядность принадлежит к умениям, которые могут легко варьироваться по отношению к разным объектам деятельности, т.е. является обобщённым общеучебным умением. Однако обобщённые умения формируются не сами по себе, а одновременно с предметными умениями. В частности на уроках русс ...

Компьютер как современное техническое средство обучения и воспитания
Персональный компьютер (ПК) — универсальное обучающее средство, которое может быть с успехом использовано на самых различных по содержанию и организации учебных и внеклассных занятиях. При этом он вписывается в рамки традиционного обучения с широким использованием всего арсенала средств обучения. П ...

Развитие познавательных способностей средствами математического образования в школе первой ступени
На современном этапе развития начальное образование ориентировано на тезис активности ребенка в процессе обучения. В этом состоит один из важнейших направлений развития общеобразовательной школы, модернизация которой предполагает ориентацию образования не только на усвоение обучающихся определенной ...