Историческая справка о четырехугольниках

Возникновение геометрии восходит к глубокой древности и было обусловлено практическими потребностями человеческой деятельности (необходимостью измерения земельных участков, измерения объемов различных тел и т.д.).

Простейшие геометрические сведения и понятия были известны еще в Древнем Египте. В этот период геометрические утверждения формулировались в виде правил, даваемых без доказательств.

С VII века до н.э. по I век н.э. геометрия как наука бурно развивалась в Древней Греции. В этот период происходило не только накопление различных геометрических сведений, но и отрабатывалась методика доказательств геометрических утверждений, а также делались первые попытки сформулировать основные первичные положения (аксиомы) геометрии, из которых чисто логическими рассуждениями выводится множество различных геометрических утверждений. Уровень развития геометрии в Древней Греции отражен в сочинении Евклида «Начала».

В этой книге впервые была сделана попытка дать систематическое построение планиметрии на базе основных неопределяемых геометрических понятий и аксиом (постулатов).

Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н.И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная.

«Начала» Евклида оказали огромное влияние на развитие математики. Эта книга на протяжении более чем двух тысяч лет была не только учебником по геометрии, но и служила отправным пунктом для очень многих математических исследований, в результате которых возникли новые самостоятельные разделы математики.

Систематическое построение геометрии обычно производится по следующему плану:

I. Перечисляются основные геометрические понятия, которые вводятся без определений.

II. Дается формулировка аксиом геометрии.

III. На основе аксиом и основных геометрических понятий формулируются остальные геометрические понятия и теоремы.

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными.

Четырехугольники бывают выпуклые (как ABCD) и невыпуклые (A1B1C1D1).

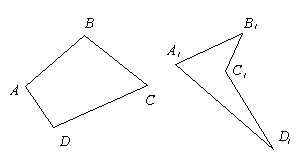
Виды четырёхугольников

Параллелограмм

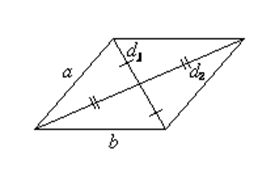
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма

противолежащие стороны равны;

противоположные углы равны;

Педагогические заметки:

Направления профориентационной работы
Мы в своей практической деятельности, направленной на оказание психологической помощи безработным, клиентам службы занятости, осуществляем технологии в рамках тренингового направления профориентационной работы. Нами разработана и реализуется программа регуляторного тренинга для безработных, основыв ...

Психолого-педагогические исследования по проблемам формирования речевых навыков на уроках иностранного языка
Прежде всего, учитель иностранного языка обучает детей способам речевой деятельности, поэтому мы говорим о коммуникативной компетенции как одной из основных целей обучения иностранным языком. Я.М. Колкер в работе «Практическая методика обучения иностранному языку» останавливается подробно на следую ...

Категория цели воспитания в педагогике
Профессиональная деятельность педагога, как любая человеческая деятельность, предваряется осознанием цели. Отсутствие цели не позволяет классифицировать работу педагога с детьми как деятельность профессионала, эта работа может быть классифицирована лишь как некоторая активность, как совокупность де ...