Историческая справка о четырехугольниках

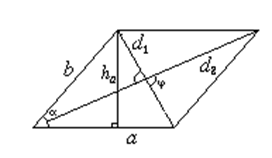
S = aha

S = ab sin

S =d1d2 sin

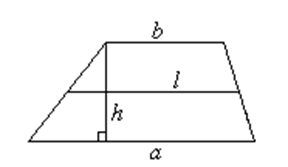
Трапеция

a и b – основания; h – расстояние между ними; l – средняя линия.

S = lh

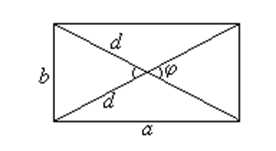
Прямоугольник

S = ab

S =d1d2 sin

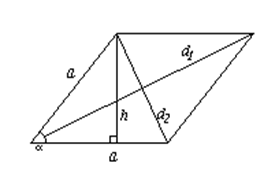
Ромб

S = aha

S = a2sin

S =d1d2

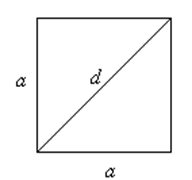
Квадрат

d – диагональ.

S = a2

S =d2

Педагогические заметки:

Основные категории педагогики
Предметом педагогической науки являются три стороны педагогической деятельности - воспитание, образование и обучение. Воспитание осуществляется в основном через межличностное общение людей и преследует цель развития мировоззрения, морали, мотивации и характера личности, формирование черт личности и ...

Организация опытно-экспериментальной работы по эколого-экономическому образованию в учебной деятельности младших школьников
Экспериментальное исследование проводилось на базе средней школы №77 г. Ульяновска. Для проведения исследования было привлечено 30 учащихся вторых классов. Контрольную группу составили 15 детей 2 «Б» класса. В экспериментальную группу вошли 15 учащихся 2 «А» класса. Экспериментальное исследование п ...

Изучение школьников в целях профориентации
Особенности памяти, внимания, чувств, воли, желаний и способностей нельзя увидеть, оценить, измерить так же, как мы видим, оцениваем многие из окружающих нас предметов. Эти и ряд других качеств психики человека нельзя непосредственно созерцать ни у себя, ни у других людей. Но в то же время различны ...