Векторные треугольники скоростей и перемещений в задачах

Кинематика изучает „геометрию” движения - математическое описание движения без анализа причин, его вызывающих. Другими словами, без выяснения вопроса, почему рассматриваемое движение происходит именно так, а не иначе, устанавливается математическое соотношение между его различными характеристиками, такими как перемещение, пройденный путь, скорость, ускорение, время движения.

При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например,

. (2.1 1)

Соответствующий (2.1 1) многоугольник (треугольник) перемещений представлен на рис.1. Изменение скорости тела

; (2.1 2)

этому выражению соответствует треугольник скоростей (рис.2).

Если тело движется с постоянным по величине и направлению ускорением , то выражение для скорости в любой момент t времени имеет вид:

; (2.1 3)

где при t = 0. В общем случае направления векторов начальной скорости и ускорения могут не совпадать. Треугольник скоростей, соответствующий выражению (2.1 3), приведен на рис.3. Вектор перемещения при этом определяется следующим образом:

. (2.1 4)

Рисунок 1. Рисунок 2. Рисунок 3.

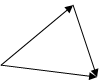
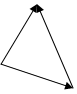
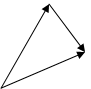
Векторные треугольники перемещений представлены на рис.4 - 6.

Рисунок 4. Рисунок 5. Рисунок 6.

Наиболее эффективно применение векторного способа, основанного на построении векторных треугольников скоростей и перемещений, в тех случаях, когда известны направления векторов ускорения и одной из скоростей (например, начальной). Это относится, в частности, к задачам о движении тепа под действием сипы тяжести.

При движении двух тел (материальных точек), зная их перемещения и относительно некоторой системы отсчета, можно вычислить перемещение второго тепа относительно первого:

. (2.1 5)

Разность скоростей теп (относительная скорость) определяется при этом выражением:

, (2.1 6)

соответствующим закону сложения скоростей Галилея:

, (2.1 7)

где и v2 - скорости первого и второго теп в неподвижной системе отсчета ("неподвижность" системы относительна), - скорость второго тела относительно первого. Векторные треугольник и параллелограммы скоростей, соответствующие формулам (2.1 6) и (2.1 7), представлены на рисунке 7.

Педагогические заметки:

Формирование технических навыков и умений у детей старшего дошкольного возраста
Изображать предметы, явления, создавать узоры, воплощать в рисунке, лепке, аппликации задуманное дети могут лишь при условии овладения техникой каждого вида изобразительной деятельности. Несмотря на то, что техническое исполнение не является главным, тем не менее, овладение правильной и разнообразн ...

Используемые программы и методики по театрально-художественной деятельности для развития коммуникативных качеств личности ребёнка дошкольника
После проведения диагностики в качестве коррекционной работы, направленной на развитие коммуникативных качеств личности ребёнка дошкольника в нашем исследовании была выбрана театрально- художественная деятельность. Для работы нами также были подобраны ряд программ и методик по театральной деятельно ...

Учебно-воспитательный коллектив как объект и субъект воспитания
Одна из важнейших его закономерностей и принципов сущности воспита­ния со­стоит в том, что развитие и формирование личности можно успешно осуществлять только в коллективе и через коллектив. Вот почему в педагогике много внимания уделялось и уделяется разработке теории и методики воспитания в коллек ...